DL之路---啃鱼书（6）

发表于2025-07-15|更新于2025-07-15

|总字数:6.4k|阅读时长:24分钟|浏览量:

卷积神经网络

卷积神经网络（Convolutional Neural Network，CNN），用于图像识别、语音识别等场景

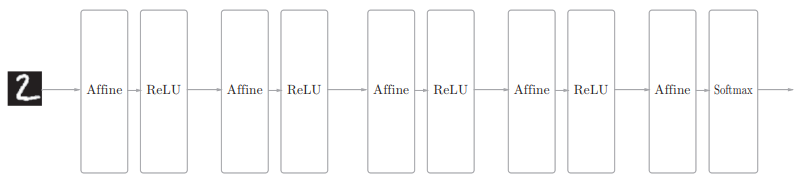
相邻层的所有神经元之间都有连接，称之为全连接，使用Affine层实现全连接层
下面是一个5层的全连接神经网络

可以看到，每个Affine层后面跟着激活函数层
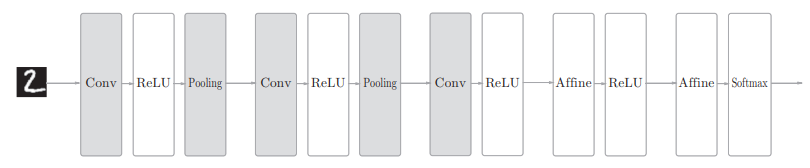
而基于CNN的神经网络结构如下

可以看到，CNN的层的连接顺序是 $Convolution - ReLU-Pooling$ ，Pooling层有时会被省略，另外，靠近输出的层中使用了之前使用了 “Affine-ReLU”组合
卷积层

回顾Affine层：

在全连接层中，相邻层的神经元全部连接在一起，输出的数量可以任意决定
它存在的一个问题是，忽视了输入数据的形状，如输入数据是图像（高、长、通道方向上的3维形状）时，输入到Affine层会将3维数据拉成1维的，无法利用与形状相关的信息

而卷积层Conv可以保持形状不变，当输入数据是图像时，卷积层会以3维数据的形式接收输入数据，并同样以3维数据的形式输出至下一层
在CNN中，有时将卷积层Conv的输入输出数据称为特征图（feature map），输入数据就叫输入特征图，输出就叫输出特征图
卷积运算

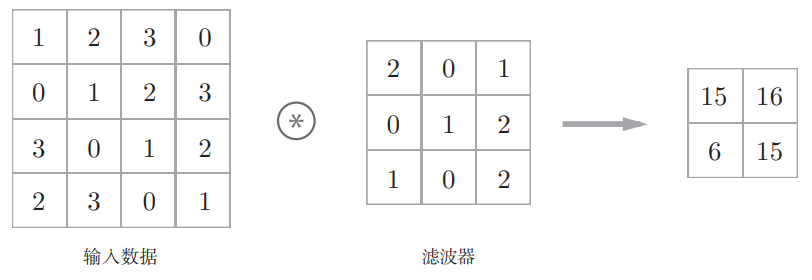
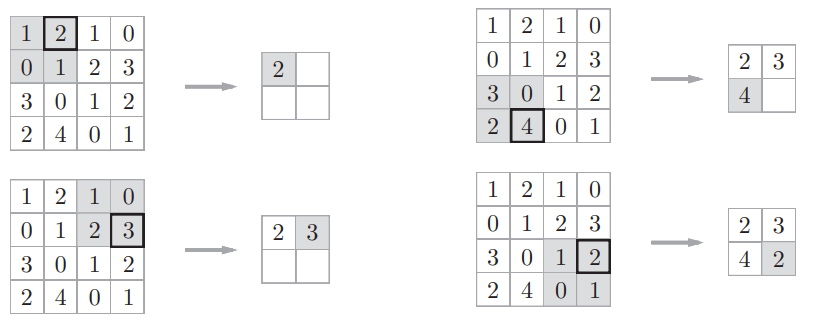
卷积层进行的处理就是卷积运算，结合例子说明（输入数据和滤波器之间的符号表示卷积运算）

这里的滤波器（filter）也被称为“卷积核（convolution kernel）”，滤波器是一个结构单位，里面的值就是权重。另外，输入数据和卷积核都是有高宽方向的形状的数据(height, weight)，卷积运算的过程如下

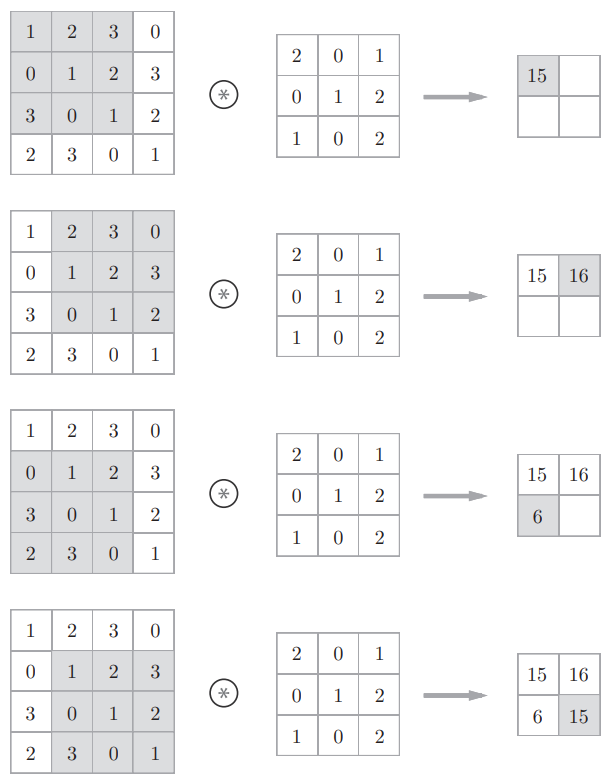
对于输入数据，卷积运算以一定间隔滑动滤波器的窗口并应用，将各个位置上滤波器的元素和输入的对应元素相乘，然后再求和（乘积累加运算），然后，将这个结果保存到输出的对应位置，所有位置进行一次，就可以得到卷积运算的输出
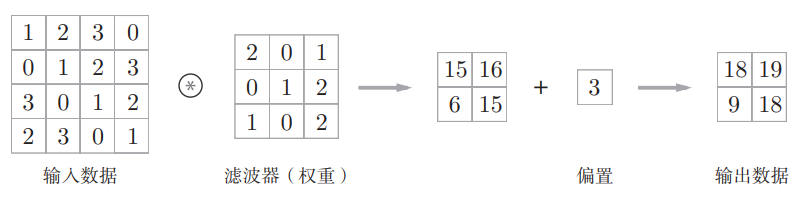
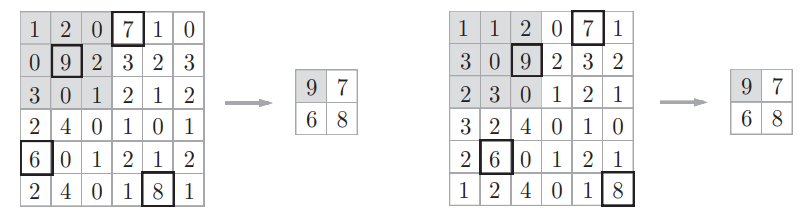
在全连接的神经网络中，除了权重参数，还存在偏置；在CNN中，滤波器的参数就对应之前的权重，且也存在偏置，包含偏执的卷积运算处理如下

上面的操作，本质上就是在进行多个 $ y = W \cdot x + b$ 运算，所以所有的输出都要 +b

填充

在进行卷积层的处理之前，有时要向输入数据的周围填入固定的数据（如0等），这称之为填充（padding）
为什么要进行填充操作呢？

通过之前的卷积操作过程，注意到，经过卷积运算的输入数据得到的输出数据，大小（空间）缩小了，而卷积层往往不止一层，多次卷积操作之后，可能会使得输出数据的大小变为1从而导致不能再进行卷积操作了（赘述）
所以，使用填充主要是为了调整输出的大小，之所以要进行填充，是因为如果每次进行卷积运算都会缩小空间（如(4,4)的输入，(3,3)的滤波器，输出是(2,2)），那么在某个时刻输出大小就有可能变为 1，导致无法再应用卷积运算

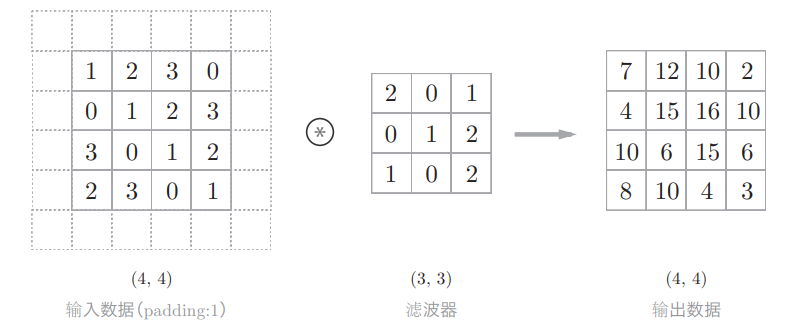
填充如何实现的，例：对大小为（4，4）的输入数据应用了幅度为1的填充

“幅度为1的填充”是指用幅度为1像素的0填充周围，填0的话直接省略不写，填充后，(4,4)的输入数据变成了(6,6)的形状

步幅

应用滤波器（卷积核）的位置间隔称为步幅（stride）
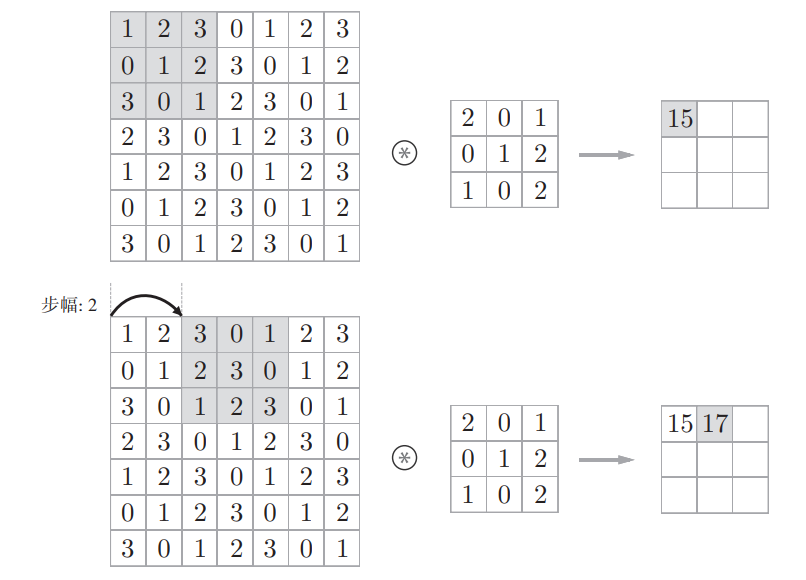
下面将应用滤波器的窗口的间隔变为2个元素

注意，步幅为2，意味着各个方向上（横向纵向）的移动都是2个元素
增大步幅后，输出大小会变小。而增大填充后，输出大小会变大，对于步幅和填充，计算输出大小

若输入大小为(H,W)，卷积核大小为（FH,FW），输出大小为(OH,OW)，填充为P，步幅为S，此时，输出大小可通过以下式子计算
$$
OH = \frac {H + 2P - FH} {S} + 1 \
OW = \frac {W + 2P - FW} {S} + 1
$$

不过有一个问题是，分式的值可能是小数（除不尽的情况），这时需要采取报错等对策，采取的深度学习框架不同，当值无法除尽时，有时会向最接近的整数四舍五入，不进行报错而继续运行

3维数据的卷积运算

对于3维数据的卷积运算，相比于2维数据的，其在纵深方向（通道方向）上特征图增加了
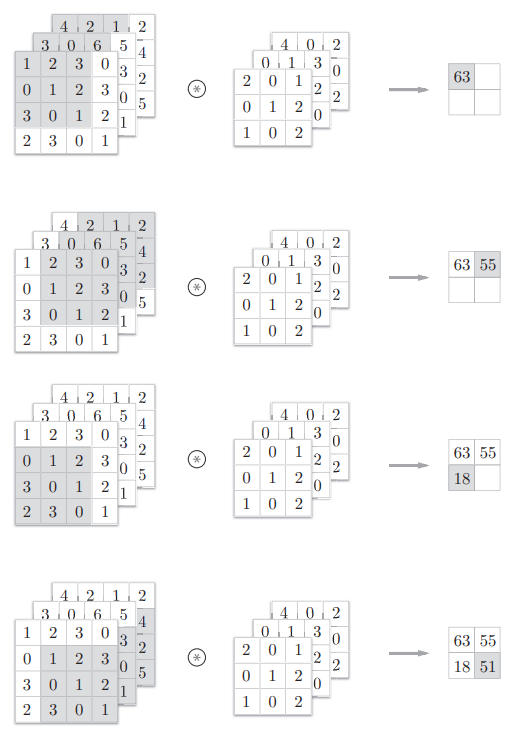
通道方向上有多个特征图时，会按通道进行输入数据和滤波器的卷积运算，并将结果相加，从而得到输出

需要注意的是，输入数据和滤波器的通道数要设为相同的值
通过立体方块来理解

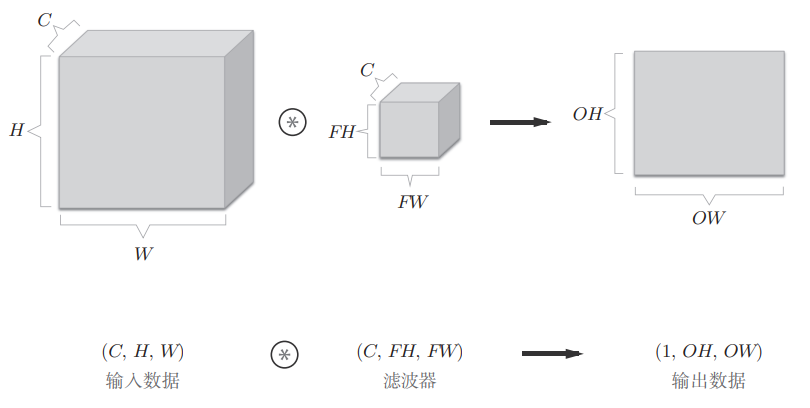
以3维数据为例，把3维数据表示为多维数组时，书写顺序是 $(channel, height, weight)$ 或 $(C,H,W)$，滤波器(卷积核)也是写作这样的形式 $(C,FH,FW)$ ，如下

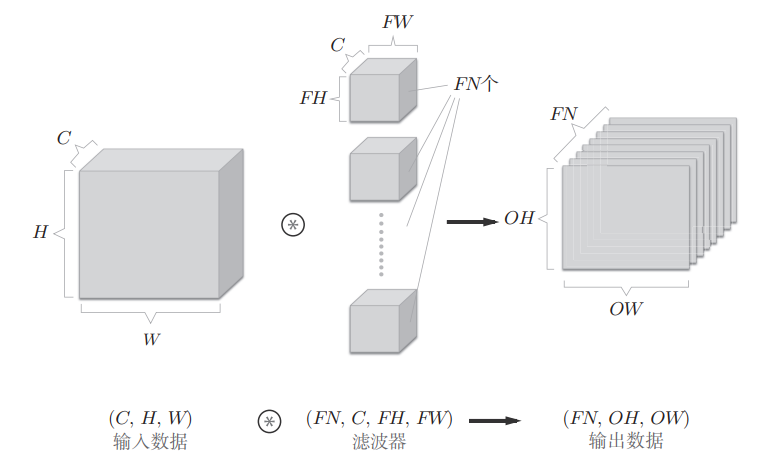
上面的输出数据是一张特征图，也即通道数为 1 的特征图，如果要在通道方向上也有多个卷积核运算的输出，就需要用到多个滤波器（权重），如下

通过使用FN个卷积核，对应的输出特征图也变成了FN个，将这FN个特征图汇集在一起，就得到了一个形状为 $(FN,OH,OW)$ 的方块，再将这个方块传递到下一层，就形成了CNN的处理流
那么4维的数据，卷积核的权重数据的书写顺序应该是 $(FC,CC,FH,FW)$ ，即卷积核个数、卷积核通道数、卷积核高、卷积核宽
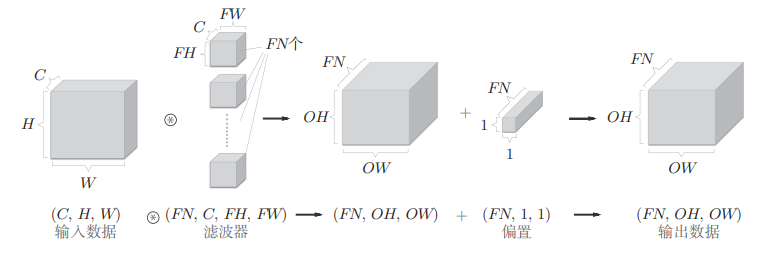
同样，也要加上偏置，如下

注意，偏置的通道数要与卷积核的个数相同

批处理

通过批处理，能够实现处理的高效化和学习时对mini-batch的对应。在卷积运算中应用批处理，需要将在各层间传递的数据保存为4维数据，即 $(batch-num,channel,height,weight)$
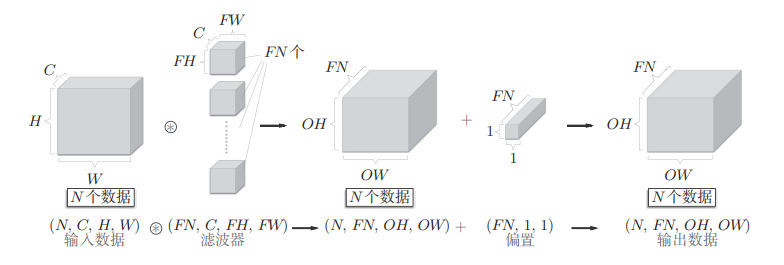
N个数据的批处理如下，

批处理将N次处理汇总成了一次进行

池化层

池化是缩小高、长方向上的空间的运算
它的主要作用是对输出特征图进行下采样(subsampling or downsampling)
它的作用是

降维、减少计算量和内存开销，当原始输出特征图尺寸较大时，池化可以有效减小后续网络层的输入大小，从而减少参数数量和计算量
提取主要特征、抑制噪声，如Max池化、Average池化、Global池化等
提高模型泛化能力，池化引入了某种程度的位置不变性(translation invariance)，使模型对小范围的平移、旋转、缩放更具鲁棒性
防止过拟合，减少特征维度，限制了网络学习过于复杂的模式，有助于抑制过拟合

池化的目的是减小特征尺寸、增强抽象能力、提高效率
补充：池化处理的就是张量，张量（tensor）就是一个具有维度的数值数组，0维是标量，1维是向量，2维是矩阵，3维及以上就是张量
下面是Max池化的处理顺序

这个例子是按照步幅为2进行池化窗口为 2x2 的Max池化操作的，处理的是输出特征图，Max池化是从目标区域（池化窗口）中取出最大值，提取显著特征
一般来说，池化的窗口大小会和步幅设定为相同值
除了Max池化，还有Average池化和Global池化，Average池化则是计算目标区域的平均值，用于平滑特征图；而Global池化是对整个特征图求平均或最大值，常用于分类前最后一层
池化层的特征

没有要学习的参数，池化层和卷积层不同，没有要学习的参数
通道数不发生变化，经过池化运算，输入数据和输出数据的通道数不会发生变化
对微小的位置变化具有鲁棒性，输入数据发生微小偏差时，池化仍会返回相同的结果，如下面的例子

当输入数据在宽度方向上只偏离1个元素时，输出仍为相同的结果，当然，根据数据的不同，有时结果也不相同

卷积层和池化层的实现

CNN中各层间传递的数据是4维数据，即 $(数据个数,通道数,高,宽)$
基于im2col的展开

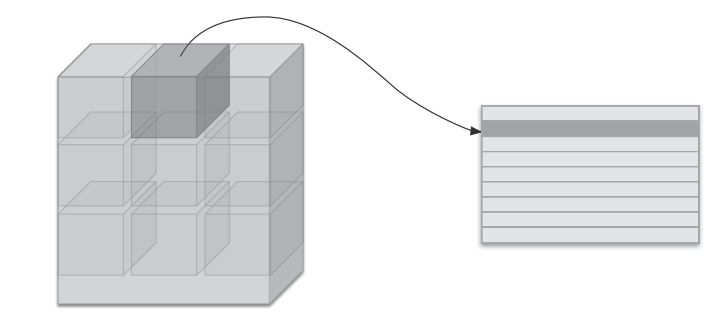
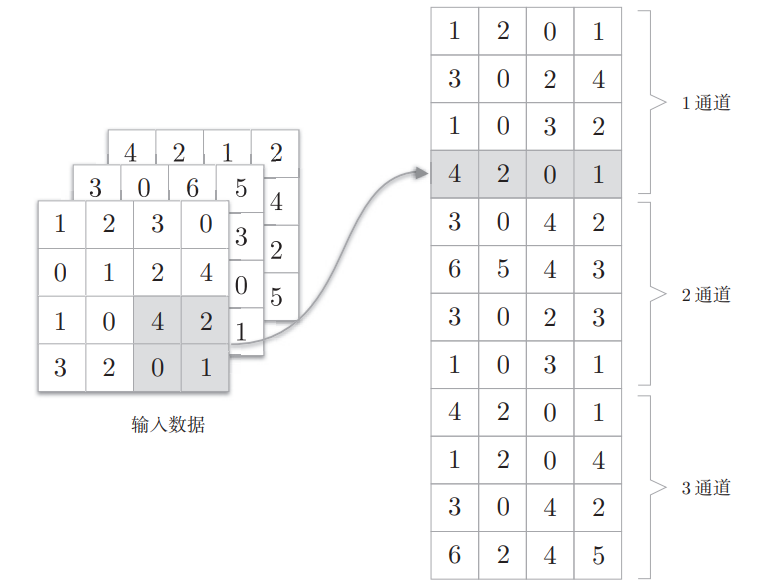
im2col是一个函数，将输入数据展开以适合滤波器（权重），对于输入数据，将应用卷积核的区域(3维方块)横向展开为1列，im2col会在所有应用卷积核的区域进行这个展开处理，如下所示

值得注意的是，滤波器的应用区域几乎都是重叠的，在此情况下，使用im2col展开后，展开后的元素个数会多于原方块(输入数据)的元素个数，因此，使用im2col的实现存在比普通的实现消耗更多内存的缺点。但，汇总成一个大的矩阵进行计算，对计算机的计算颇有益处，因为可以有效地利用线性代数库
另外，im2col 意为 image to column，即图像到矩阵
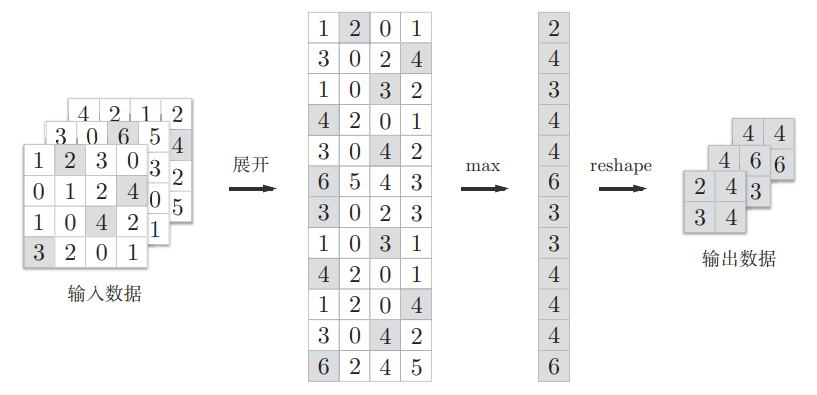
im2col的处理过程如下

从原始输入图像数据中提取所有滑动窗口区域（patch）

将每个patch展开成1行

再将所有的patch行拼接成一个矩阵（im2col矩阵）

将卷积核拉平成一个列向量

进行矩阵乘法（类似于Affine层进行的处理）

再reshape成输出特征图的形状

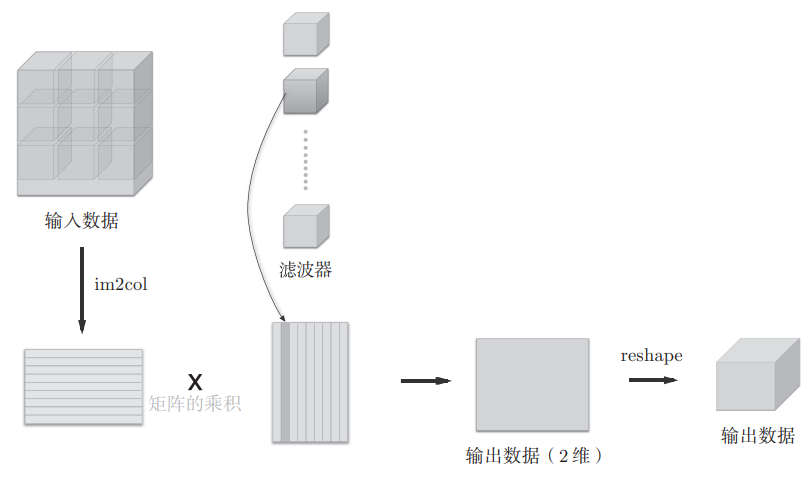
使用im2col展开输入数据后，之后就只需将卷积层的滤波器（权重）纵向展开为1列，并计算2个矩阵的乘积即可，这和全连接层的Affi ne层进行的处理基本相同
使用im2col的卷积运算的卷积核处理过程如下

因为CNN中数据会保存为4维数组，所以要将2维输出数据转换(reshape)为合适的形状，这就是卷积层的实现流程

卷积层的实现

在卷积层的实现过程中，有以下几个点需要注意

im2col函数得到的是col，这个col表示 $(输出区域数,每个区域展开后元素个数)$ ，这个输出区域数其实就是 H_out * W_out，它就是经过im2col展开后得到的行数。而第2个参数就是卷积核大小 * 通道数，即 $FH * FW * C$

卷积层的实现的类中的forward方法里，im2col展开处理后的数据形状 col.shape=(N*out_h*out_w, C*FH*FW)，卷积核展开之后的形状 col_W.shape = (C*FH*FW, FN)，那么 dot(col, col_W) 得到的输出的形状就是 out.shape = (N*out_h*out_w, FN)，这表示为：每一张输入图像，每一个输出位置(out_h*out_w)个，对每一个卷积核（共FN个）都得到一个输出数值。再将得到的输出out还原为 4D 卷积输出张量结构。注意：这里的N是batch_size，也是输入图像的个数；FN是卷积核的个数，也是这层卷积层的输出通道数

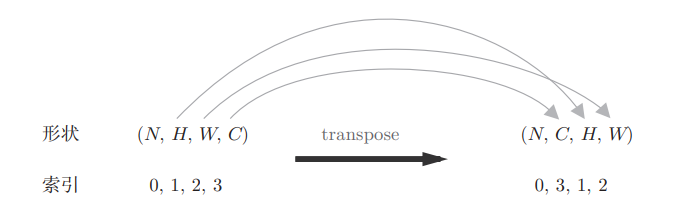
将out还原为4D卷积输出张量结构，这里就有一个新的问题，为什么不能直接使用 reshape 将out.shape变为 (N, FN, out_h, out_w) ？这是因为 reshape 只是重新排列元素的形状，不能改变维度的排列顺序（轴顺序），要改变轴顺序必须使用 transpose，out.shape = ( N * out_h * out_w, FN )，axis=0:N*out_h*out_w，axis=1:FN，reshape不会打乱数据顺序，而transpose是要调整轴的排列的，transpose(0,3,1,2)这里的数值是reshape之后 0N1H2W3C 的下标，不是实际值，最后要调整为NCHW（0,3,1,2），如下图

在进行卷积层的反向传播时，必须进行im2col的逆处理，这里使用一个col2im函数，代码在code里

池化层的实现

池化层的实现和卷积层相同，都使用im2col展开输入数据，不过，池化的情况下，在通道方向上是独立的，这一点和卷积层不同，也即池化的应用区域按通道单独展开

然后进行Max池化

CNN的实现

有几点需要注意
初始化方法中，池化输出大小的代码如下
1
pool_output_size = int(filter_num * (conv_output_size / 2) * (conv_output_size / 2))
其中 conv_output_size/2 是因为后面定义的池化窗口大小为2x2，且stride=2，所以池化后输出的高宽会变为原来的一半，池化层的设定如下
1
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
初始化方法中，参数 weight_init_std=0.01 的作用，这是为了控制权重初始化的“数值范围”，防止信号和梯度在网络中“放大或消失”，从而保持网络稳定训练，np.random.randn()是均值为0、标准差为1的正态分布，数值范围在-3到3，这有可能会导致梯度消失或爆炸。而乘以0.01后就变为了均值为0，标准差为0.01的正态分布，则会更稳定一点

CNN的可视化

卷积层的滤波器会提取边缘或斑块等原始信息

具有代表性的CNN

LeNet
AlexNet

Code

卷积层的实现

class Convolution:
 """
 卷积层，实现前向和反向传播。
 """
 def __init__(self, W, b, stride=1, pad=0):
     self.W = W  # 卷积核权重，形状(FN, C, FH, FW)
     self.b = b  # 偏置，形状(FN,)
     self.stride = stride  # 步幅
     self.pad = pad        # 填充
     self.x = None   # 输入
     self.col = None # im2col展开后的输入
     self.col_W = None # 展开后的卷积核
     self.dW = None  # 权重梯度
     self.db = None  # 偏置梯度

 def forward(self, x):
     """
     前向传播：im2col展开输入，矩阵乘法实现卷积。
     """
     FN, C, FH, FW = self.W.shape  # 卷积核参数
     N, C, H, W = x.shape          # 输入参数
     out_h = 1 + int((H + 2*self.pad - FH) / self.stride)  # 输出高
     out_w = 1 + int((W + 2*self.pad - FW) / self.stride)  # 输出宽
     col = im2col(x, FH, FW, self.stride, self.pad)  # 输入展开
     col_W = self.W.reshape(FN, -1).T  # 卷积核展开
     out = np.dot(col, col_W) + self.b  # 矩阵乘法+偏置
     out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)  # 还原输出形状
     self.x = x
     self.col = col
     self.col_W = col_W
     return out

 def backward(self, dout):
     """
     反向传播：计算输入、权重、偏置的梯度。
     """
     FN, C, FH, FW = self.W.shape
     dout = dout.transpose(0,2,3,1).reshape(-1, FN)  # 调整dout形状
     self.db = np.sum(dout, axis=0)  # 偏置梯度
     self.dW = np.dot(self.col.T, dout)  # 权重梯度
     self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)  # 还原权重形状
     dcol = np.dot(dout, self.col_W.T)  # 输入展开后的梯度
     dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)  # 还原输入形状
     return dx

col2im

# col2im: 将im2col展开的二维矩阵还原为原始多维图像数据
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
    """
    将im2col展开的二维矩阵还原为原始的多维图像数据。

    Parameters
    ----------
    col : 展开后的二维矩阵
    input_shape : 原始输入数据的形状（如：(10, 1, 28, 28)）
    filter_h : 滤波器高度
    filter_w : 滤波器宽度
    stride : 步幅
    pad : 填充

    Returns
    -------
    img : 还原后的多维图像数据
    """
    N, C, H, W = input_shape
    out_h = (H + 2*pad - filter_h)//stride + 1  # 输出高度
    out_w = (W + 2*pad - filter_w)//stride + 1  # 输出宽度
    # 还原为im2col前的形状
    col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)

    # 初始化还原后的图像，注意填充和步幅的影响
    img = np.zeros((N, C, H + 2*pad + stride - 1, W + 2*pad + stride - 1))
    # 将每个patch累加到对应的位置
    for y in range(filter_h):
        y_max = y + stride*out_h
        for x in range(filter_w):
            x_max = x + stride*out_w
            img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]

    # 去除填充部分，返回原始大小
    return img[:, :, pad:H + pad, pad:W + pad]

池化层的实现

class Pooling:
 """
 池化层，实现最大池化的前向和反向传播。
 """
 def __init__(self, pool_h, pool_w, stride=2, pad=0):
     self.pool_h = pool_h  # 池化窗口高
     self.pool_w = pool_w  # 池化窗口宽
     self.stride = stride  # 步幅
     self.pad = pad        # 填充
     self.x = None         # 输入
     self.arg_max = None   # 最大值索引

 def forward(self, x):
     """
     前向传播：im2col展开后做最大池化。
     """
     N, C, H, W = x.shape
     out_h = int(1 + (H - self.pool_h) / self.stride)  # 输出高
     out_w = int(1 + (W - self.pool_w) / self.stride)  # 输出宽
     col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)  # 输入展开
     col = col.reshape(-1, self.pool_h*self.pool_w)  # 每个池化区域展平成一行
     arg_max = np.argmax(col, axis=1)  # 最大值索引
     out = np.max(col, axis=1)         # 最大值
     out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)  # 还原输出形状
     self.x = x
     self.arg_max = arg_max
     return out

 def backward(self, dout):
     """
     反向传播：最大池化的反向传播，将梯度传递到最大值位置。
     """
     dout = dout.transpose(0, 2, 3, 1)  # 调整dout形状
     pool_size = self.pool_h * self.pool_w
     dmax = np.zeros((dout.size, pool_size))  # 初始化梯度
     dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()  # 只在最大值位置赋值
     dmax = dmax.reshape(dout.shape + (pool_size,)) 
     dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)  # 展平成二维
     dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)  # 还原输入形状
     return dx

简单的CNN例子

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 添加父目录到模块搜索路径，便于导入common模块
import pickle
import numpy as np
from collections import OrderedDict
from common.layers import *
from common.gradient import numerical_gradient


class SimpleConvNet:
    """
    简单卷积神经网络（ConvNet）实现：
    网络结构为 conv - relu - pool - affine - relu - affine - softmax。
    支持参数保存与加载，支持数值梯度和反向传播梯度。
    """
    def __init__(self, input_dim=(1, 28, 28), 
                 conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
                 hidden_size=100, output_size=10, weight_init_std=0.01):
        """
        初始化网络参数和各层。
        input_dim: 输入数据的形状 (通道数, 高, 宽)
        conv_param: 卷积层参数字典，包括filter_num, filter_size, pad, stride
        hidden_size: 隐藏层神经元数
        output_size: 输出类别数
        weight_init_std: 权重初始化标准差
        """
        filter_num = conv_param['filter_num']
        filter_size = conv_param['filter_size']
        filter_pad = conv_param['pad']
        filter_stride = conv_param['stride']
        input_size = input_dim[1]
        # 计算卷积层输出尺寸
        conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
        # 计算池化层输出尺寸（池化窗口为2x2，步幅2）
        pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))

        # 权重初始化
        self.params = {}
        self.params['W1'] = weight_init_std * \
                            np.random.randn(filter_num, input_dim[0], filter_size, filter_size)  # 卷积核权重
        self.params['b1'] = np.zeros(filter_num)  # 卷积核偏置
        self.params['W2'] = weight_init_std * \
                            np.random.randn(pool_output_size, hidden_size)  # 全连接层1权重
        self.params['b2'] = np.zeros(hidden_size)  # 全连接层1偏置
        self.params['W3'] = weight_init_std * \
                            np.random.randn(hidden_size, output_size)  # 全连接层2权重
        self.params['b3'] = np.zeros(output_size)  # 全连接层2偏置

        # 构建网络层（有序字典保证前向/反向顺序）
        self.layers = OrderedDict()
        self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
                                           conv_param['stride'], conv_param['pad'])  # 卷积层
        self.layers['Relu1'] = Relu()  # 激活层
        self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)  # 池化层
        self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])  # 全连接层1
        self.layers['Relu2'] = Relu()  # 激活层
        self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])  # 全连接层2

        self.last_layer = SoftmaxWithLoss()  # 最后一层为softmax+损失

    def predict(self, x):
        """
        前向传播，输出网络预测结果。
        x: 输入数据
        返回：输出结果
        """
        for layer in self.layers.values():
            x = layer.forward(x)
        return x

    def loss(self, x, t):
        """
        计算损失函数值。
        x: 输入数据
        t: 标签（监督信号）
        返回：损失值
        """
        y = self.predict(x)
        return self.last_layer.forward(y, t)

    def accuracy(self, x, t, batch_size=100):
        """
        计算预测精度。
        x: 输入数据
        t: 标签
        batch_size: 批大小
        返回：精度（0~1）
        """
        if t.ndim != 1 : t = np.argmax(t, axis=1)  # 若为one-hot则转为标签索引
        acc = 0.0
        for i in range(int(x.shape[0] / batch_size)):
            tx = x[i*batch_size:(i+1)*batch_size]
            tt = t[i*batch_size:(i+1)*batch_size]
            y = self.predict(tx)
            y = np.argmax(y, axis=1)
            acc += np.sum(y == tt)  # 统计预测正确个数
        return acc / x.shape[0]

    def numerical_gradient(self, x, t):
        """
        用数值微分法计算各层参数的梯度。
        x: 输入数据
        t: 标签
        返回：包含各层权重和偏置梯度的字典
        """
        loss_w = lambda w: self.loss(x, t)
        grads = {}
        for idx in (1, 2, 3):
            grads['W' + str(idx)] = numerical_gradient(loss_w, self.params['W' + str(idx)])  # 权重梯度
            grads['b' + str(idx)] = numerical_gradient(loss_w, self.params['b' + str(idx)])  # 偏置梯度
        return grads

    def gradient(self, x, t):
        """
        用反向传播法计算各层参数的梯度。
        x: 输入数据
        t: 标签
        返回：包含各层权重和偏置梯度的字典
        """
        # 前向传播，计算损失
        self.loss(x, t)
        # 反向传播，计算梯度
        dout = 1
        dout = self.last_layer.backward(dout)
        layers = list(self.layers.values())
        layers.reverse()  # 反向传播需逆序
        for layer in layers:
            dout = layer.backward(dout)
        # 收集各层的权重和偏置梯度
        grads = {}
        grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
        grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
        grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
        return grads
        
    def save_params(self, file_name="params.pkl"):
        """
        保存网络参数到文件。
        file_name: 文件名
        """
        params = {}
        for key, val in self.params.items():
            params[key] = val
        with open(file_name, 'wb') as f:
            pickle.dump(params, f)

    def load_params(self, file_name="params.pkl"):
        """
        从文件加载网络参数。
        file_name: 文件名
        """
        with open(file_name, 'rb') as f:
            params = pickle.load(f)
        for key, val in params.items():
            self.params[key] = val
        # 更新各层的权重和偏置
        for i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):
            self.layers[key].W = self.params['W' + str(i+1)]
            self.layers[key].b = self.params['b' + str(i+1)]

手写数字识别的CNN

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 将父目录添加到sys.path，便于导入模块
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from simple_convnet import SimpleConvNet
from common.trainer import Trainer

# 加载MNIST数据集（不展开，保持(N, 1, 28, 28)的形状）
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=False)

# 如果训练速度较慢，可以通过取消注释下方代码来减少数据量
# x_train, t_train = x_train[:5000], t_train[:5000]
# x_test, t_test = x_test[:1000], t_test[:1000]

max_epochs = 20  # 训练的总轮数

# 初始化卷积神经网络
network = SimpleConvNet(
    input_dim=(1,28,28),  # 输入数据的形状：(通道数，高，宽)
    conv_param={'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},  # 卷积层参数
    hidden_size=100,  # 隐藏（全连接）层的神经元数量
    output_size=10,   # 输出类别数（数字0-9）
    weight_init_std=0.01  # 权重初始化的标准差
)

# 设置训练器
trainer = Trainer(
    network, x_train, t_train, x_test, t_test,
    epochs=max_epochs, mini_batch_size=100,  # 训练轮数和每个小批量的样本数
    optimizer='Adam', optimizer_param={'lr': 0.001},  # 优化器及其学习率
    evaluate_sample_num_per_epoch=1000  # 每轮评估的样本数
)

# 开始训练
trainer.train()

# 保存训练好的网络参数到文件
network.save_params("params.pkl")
print("Saved Network Parameters!")

# 绘制训练集和测试集的准确率随轮数变化的曲线
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, trainer.train_acc_list, marker='o', label='train', markevery=2)
plt.plot(x, trainer.test_acc_list, marker='s', label='test', markevery=2)
plt.xlabel("epochs")  # 横坐标为训练轮数
plt.ylabel("accuracy")  # 纵坐标为准确率
plt.ylim(0, 1.0)  # 设置y轴范围
plt.legend(loc='lower right')  # 图例位置
plt.show()

CNN的可视化

import os, sys
import numpy as np
sys.path.append('../../py_pro/DL/ch07/')
import matplotlib.pyplot as plt
from simple_convnet import SimpleConvNet


# 可视化卷积核（滤波器）权重的函数
def filter_show(filters, nx=8, margin=3, scale=10):
    """
    显示卷积层的滤波器（权重），以灰度图形式排列。
    参数：
        filters: 卷积核权重，形状为 (FN, C, FH, FW)
        nx: 每行显示的滤波器数量
        margin: 图像之间的间隔（未使用）
        scale: 图像缩放比例（未使用）
    """
    FN, C, FH, FW = filters.shape  # FN:滤波器个数, C:通道数, FH:高, FW:宽
    ny = int(np.ceil(FN / nx))     # 计算需要的行数

    fig = plt.figure()
    # 调整子图间距，去除边距和间隔
    fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)

    for i in range(FN):
        # 在ny行nx列的子图中添加第i+1个子图，不显示坐标轴刻度
        ax = fig.add_subplot(ny, nx, i+1, xticks=[], yticks=[])
        # 显示第i个滤波器的第一个通道（通常为灰度图）
        ax.imshow(filters[i, 0], cmap=plt.cm.gray_r, interpolation='nearest')
    plt.show()

# 创建卷积神经网络实例
network = SimpleConvNet()
# 显示随机初始化后的第一层卷积核权重
filter_show(network.params['W1'])

# 加载训练后保存的参数
network.load_params("../../py_pro/DL/ch07/params.pkl")
# 显示训练后第一层卷积核权重
filter_show(network.params['W1'])

如懂！！！

文章作者: yanzu

文章链接: http://yanzu.tech/2025/07/15/26/