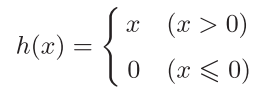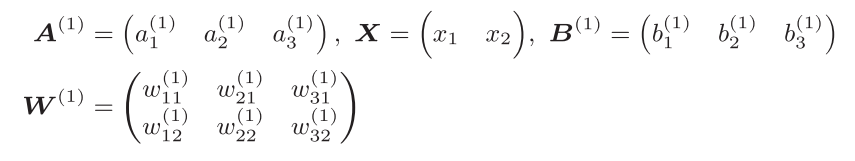神经网络

神经网络的一个重要性质是它可以自动地从数据中学习到合适的权重参数

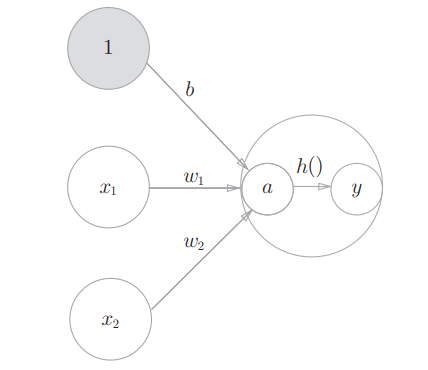
激活函数

它会将输入信号的总和转换为输出信号，它决定了以何种方式激活输入信号的总和

朴素感知机和神经网络的主要区别就在于激活函数的不同

计算过程如下:

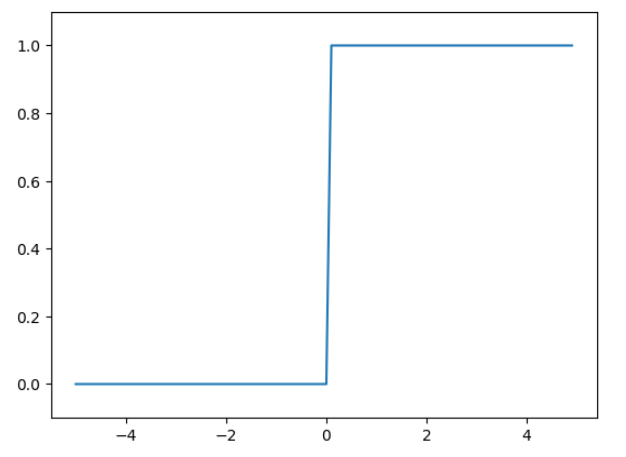
阶跃函数：一旦输入超过阈值，就切换输出（sign符号函数，朴素感知机的激活函数）

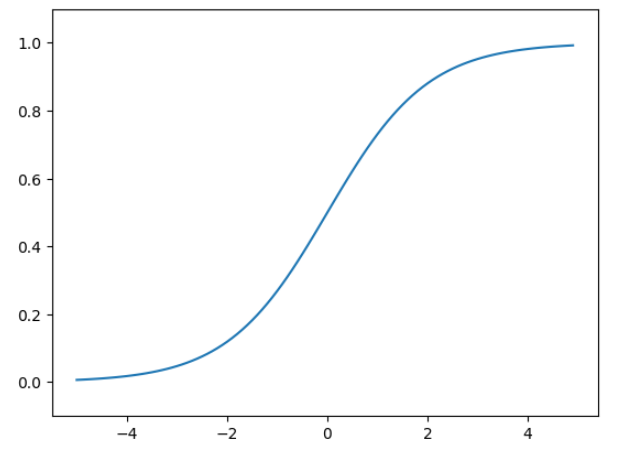
sigmoid函数

神经网络中一个常用的激活函数就是sigmoid函数，其表达式如下：

$$
h(x) = \frac {1}{1 + exp(-x)}
$$

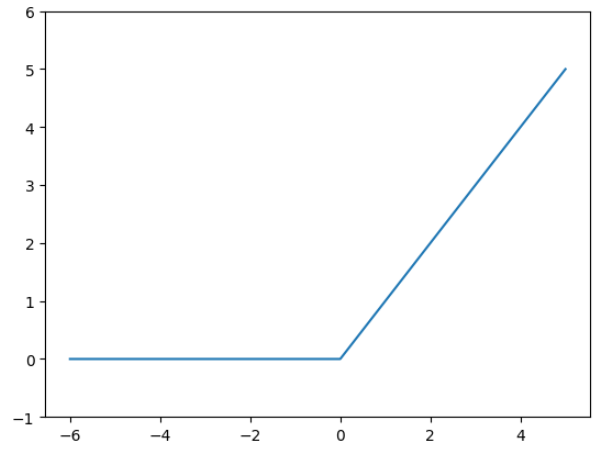
ReLU函数

自变量 $ x > 0 $ 时，直接输出该值，$ x \le 0 $ 时，输出0

它的表达式如下：

3层神经网络的实现

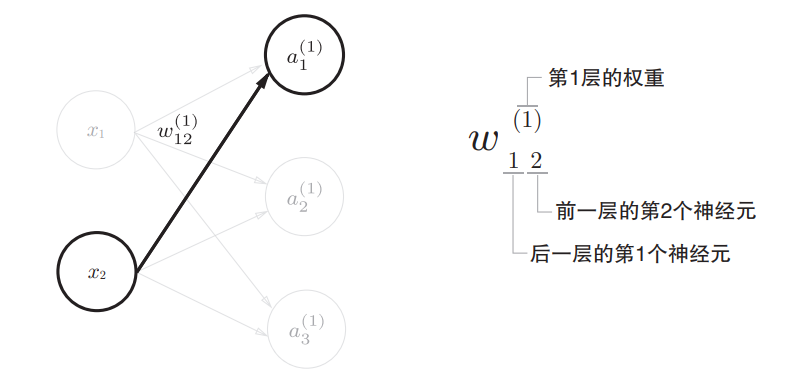
首先引入一个概念符号确认

下面是权重符号的表示，

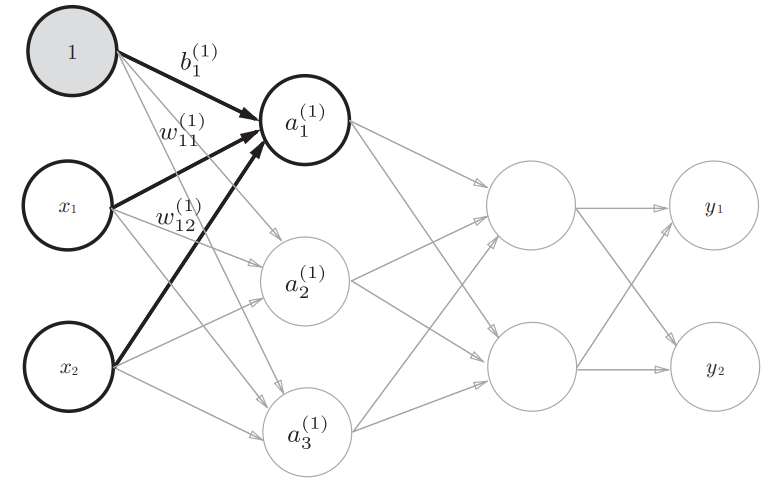
各层间信号传递的实现

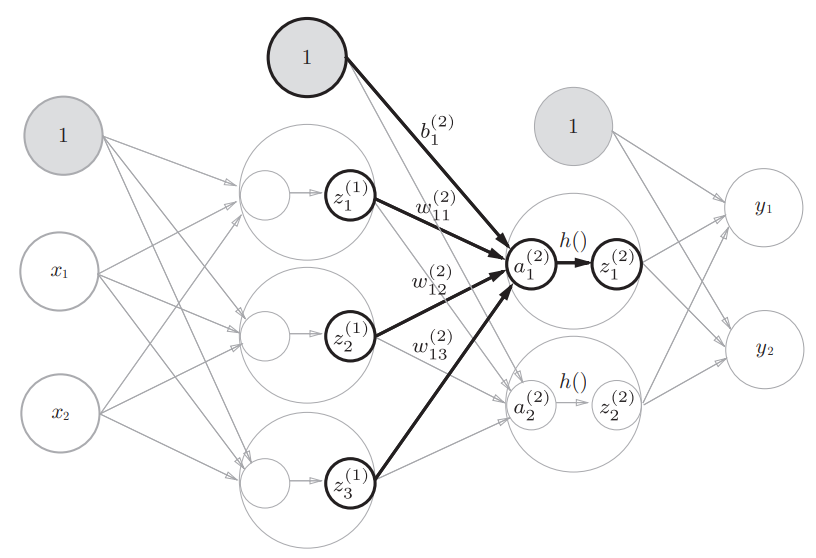
首先是第0层到第1层之间信号传递的实现

注意，偏置 $ b $ 的右下角的索引号只有一个，这是因为前一层的偏置神经元（神经元1）只有一个，右下角的索引是表示前一个神经元的，对应到权重的符号表示是 $ b^\left[(1)\right]_{None,1} $ ，因为本身a本身就在一个神经元上了，所以前一个索引是None

$ a_1 $的表达式如下：

$$
a_1^{(1)} = w_{11}^{(1)} x_1 + w_{12}^{(1)} x_2 + b_1^{(1)}
$$

使用矩阵的乘法运算表示第1层的加权和

$$
A^{(1)} = XW^{(1)} + B^{(1)}
$$

其中，$ A^{(1)},X,B^{(1)},W^{(1)} $如下所示

$W_i$的每一列对应一个$ a_i $

第1层到第2层之间信号传递的实现

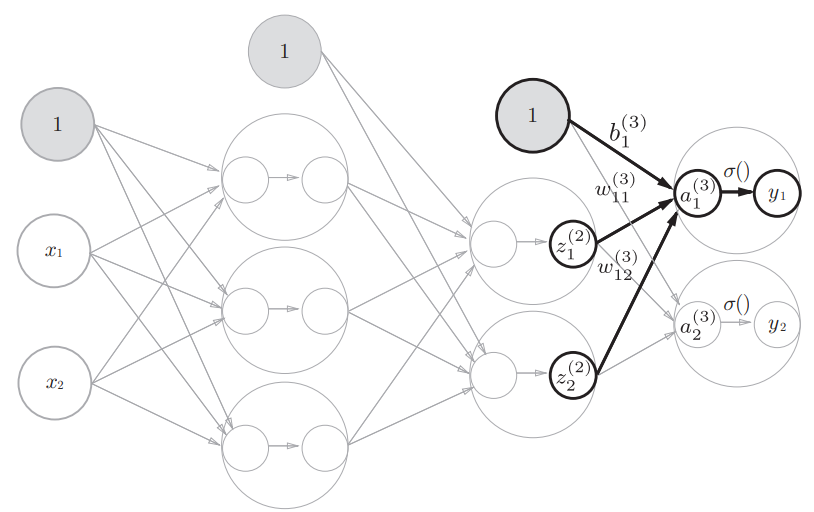
第2层到输出层之间信号传递的实现

输出层的激活函数一般用 $ \sigma() $ 来表示，隐藏层的激活函数一般用 $ h() $ 来表示

另外，输出层所使用的激活函数要根据求解问题的性质来确定，一般情况下，回归问题可以使用恒等函数，二元分类问题可以使用 $sigmoid$ 函数，多元分类问题可以使用 $softmax$函数

输出层的设计

机器学习的问题大致可以分为分类问题和回归问题,分类问题是数 据属于哪一个类别的问题；而回归问题是根据某个输入预测一个（连续的）数值的问题

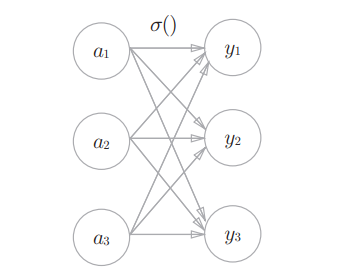
$softmax$函数（输出层的激活函数）

分类问题中使用该函数，表达式如下：

$$
\sigma = y_k = \frac {exp(a_k)} {\sum^{n}_{i = 1} exp(a_i)}
$$

这个式子表示：假设输出层共有$n$个神经元，计算第$k$个神经元的输出$y_k$

可以看出，输出层的各个神经元都受到所有输入信号的影响

注意到，上面这种形式的$softmax$函数有一个致命问题，那就是指数部分容易发生溢出

为此，对其进行改进

在进行$softmax$的指数的运算时，加上（或者减去）某个常数并不会改变运算的结果，这里的$C’$可以使用任何值，但是为了防止溢出，一般会使用输入信号中的最大值

$softmax$函数的特征，其输出是0.0到1.0之间的实数，且输出值的总和是1，这是它的一个重要性质，正因如此，一般把$softmax$的输出解释为 概率

通过使用$softmax$函数，我们可以用概率的（统计的）方法处理问题

另外，即便使用了$softmax$函数，各个元素之间的大小关 系也不会改变，因为指数函数$ y = exp(x) $是单调递增函数

一般而言，神经网络只把输出值最大的神经元所对应的类别作为识别结果，且即便使用$softmax$函数，输出值最大的神经元的位置也不会变，因此，神经网络在进行分类时，输出层的$softmax$函数可以省略（还有个原因是，指数函数的运算需要一定的计算机运算量）

求解机器学习问题的步骤可以分为学习和推理两个阶段，首先，在学习阶段进行模型的学习，然后，在推理阶段，用学到的模型对未知的数据进行推理（分类）

手写数字识别

one-hot表示是仅正确解标签为1，其余皆为0的数组

pickle可以可以将程序运行中的对象保存为文件，如果加载保存过的pickle文件，可以立刻复原之前程序运行中的对象（Numpy数组），使用pickle.load()可以直接还原所有数据结构

argmax(np.array, axis)函数可以取出数组中的最大值的索引，axis=1指定沿着行方向寻找最大值

正规化（normalization）：把数据限定到某个范围内的处理

预处理（pre-processing）：对神经网络的输入数据进行某种既定的转换

数据白化（whitening）：将数据整体的分布形状均匀化的方法

批处理

code

阶跃函数的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import numpy as np
def step_fun(x):
 y = x > 0
 return y.astype(np.int)

# y = x > 0是什么意思
# 对numpy数组进行bool运算，它会对数组内的每个元素做bool运算，得到一个对应bool值的bool数组，不是浮点型数组了
x = np.array([-1.0, 1.0, 2.0])
print(x)
y = x > 0
print(y)
# astype()函数可以转换numpy数组的类型，需要对int指定精度，可以是32，也可以是64
y = y.astype(np.int32)
print(y)

阶跃函数的图像

1
2
3
4
5
6
7
8
9
10
11
import numpy as np
import matplotlib.pylab as plt

def step_fun(x):
 return np.array(x > 0, dtype=np.int32)

x = np.arange(-5.0, 5.0, 0.1)
y = step_fun(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # 指定y轴范围
plt.show()

sigmoid函数的实现

1
2
3
4
5
6
def sigmoid(x):
 return 1 / (1 + np.exp(-x))


x = np.array([-1.0, 1.0, 2.0])
print(sigmoid(x))

sigmoid函数图像

1
2
3
4
5
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

可以看到，阶跃函数和sigmoid函数的几个共同点：

一是，当输入信号为重要信息时，阶跃函数和sigmoid函数都会输出较大的值；当输入信号为不重要的信息时，两者都输出较小的值

另一个是，不管输入信号有多小，或者有多大，输出信号的值都在0到1之间

另外，两者均是非线性函数，不管是朴素感知机还是神经网络，其激活函数必须是非线性函数，不能是线性函数

ReLU函数的实现

1
2
3
4
5
6
def relu(x):
 return np.maximum(0, x)


x = np.array([-1.0, 1.0, 2.0])
print(relu(x))

ReLU函数的的图像

1
2
3
4
5
x = np.arange(-6.0, 6.0, 1.0)
y = relu(x)
plt.plot(x, y)
plt.ylim(-1.0, 6.0)
plt.show()

多维数组的运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 一维数组
import numpy as np
A = np.array([1, 2, 3, 4])
print(A)
print(np.ndim(A)) # 输出数组的维数
print(np.shape(A)) # 输出数组的形状，其结果是一个元组
print(A.shape) # 另外一种方式
print(A.shape[0])

# 二维数组，注意二维以及高维数组还需要一个额外的中括号括起来
B = np.array([[1, 2], [3, 4], [5, 6]])
print(B)
print(np.ndim(B)) # 输出数组的维数
print(np.shape(B)) # 输出数组的形状，其结果是一个元组
print(B.shape) # 另外一种方式
print(B.shape[1]) # shape[0]是数组的行数，shape[1]是数组的列数

矩阵乘法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 2 * 2 的矩阵乘法
A = np.array([[1, 2], [3, 4]])
print(A.shape)
B = np.array([[2, 3], [4, 5]])
print(B.shape)
print(np.dot(A, B)) # dot()接收两个numpy数组作为参数，返回数组的乘积

# 2*3 和 3*2 的矩阵乘法
A = np.array([[1, 2, 3], [4, 5, 6]])
print(A.shape)
B = np.array([[1, 2],[3, 4], [5, 6]])
print(B.shape)
print(np.dot(A, B)) # dot()接收两个numpy数组作为参数，返回数组的乘积
print(A @ B)

# 对于一维numpy数组的乘法运算，同样是借助了广播功能
A = np.array([[1, 2],[3, 4], [5, 6]])
print(A.shape)
B = np.array([7, 8])
print(B.shape)
print(np.dot(A, B))

神经网络的内积

1
2
3
4
5
6
X = np.array([1, 2])
print(X.shape)
W = np.array([[1, 3, 5], [2, 4, 6]])
print(W.shape)
Y = np.dot(X, W)
print(Y)

第0层到第1层之间信号传递的实现

1
2
3
4
5
6
7
8
9
10
X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3])
print(W1.shape)
print(X.shape)
print(B1.shape)
A1 = np.dot(X, W1) + B1
print(A1)
Z1 = sigmoid(A1)
print(Z1)

第1层到第2层之间信号传递的实现

1
2
3
4
5
6
7
8
9
10
W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])
print(Z1.shape)
print(W2.shape)
print(B2.shape)
# Z2 从第一层的输出变成了第二层的输入了，新的(x1, x2, x3)
A2 = np.dot(Z1, W2) + B2
print(A2)
Z2 = sigmoid(A2)
print(Z2)

第2层到输出层之间信号传递的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 注意，这两层之间的激活函数与之前隐藏层的有所不同了
# 这里的激活函数是恒等函数，就是输入是什么输出就是什么
def identify_fun(x):
    return x

W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])
print(W3.shape)
print(B3.shape)

A3 = np.dot(Z2, W3) + B3
Y = identify_fun(A3)
print(A3.shape)
print(Y)

写成函数形式，实现3层神经网络

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])
    
    return network


def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identify_fun(a3)
    
    return y


network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)

$softmax$函数的实现

1
2
3
4
5
6
7
8
9
10
def softmax(a):
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    
    return y


a = np.array([0.3, 2.9, 4.0])
print(softmax(a))

改进后的$softmax$的实现

1
2
3
4
5
6
7
8
9
10
11
def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    
    return y


a = np.array([1010, 1000, 990])
print(softmax(a))

手写数字识别

1
2
3
4
5
6
7
8
9
10
11
import sys
sys.path.append('../../py_pro/DL/') # 指定获取mnist数据集的脚本路径
import numpy as np
from dataset.mnist import load_mnist
# (训练图像，训练标签)，(测试图像，测试标签)
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True)

print(x_train.shape)
print(t_train.shape)
print(x_test.shape)
print(t_test.shape)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import os, sys
sys.path.append('../../py_pro/DL/') # 指定获取mnist数据集的脚本路径
import numpy as np
from dataset.mnist import load_mnist
from PIL import Image

def img_show(img):
    pil_img = Image.fromarray(np.uint8(img))
    pil_img.show()


(x_train, t_train), (x_test, t_test) = load_mnist(normalize=False, flatten=True)
img = x_train[0]
label = t_train[0]
print(label)

print(img.shape)
img = img.reshape(28, 28)
print(img.shape)

img_show(img)

神经网络的推理处理

神经网络的输入层有784个神经元，输出层有10个神经元，784是图片像素是28*28，10是0~910种类别，有2个隐藏层，神经元数量分别是50、100，这个可以是任意值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import pickle
def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=False, flatten=True)
    return x_test, t_test


def init_network():
    with open('../../py_pro/DL/ch03/sample_weight.pkl', 'rb') as f:
        network = pickle.load(f)
    return network


def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)

    return y

x, t = get_data()
network = init_network()

accuracy_cnt = 0
for i in range(len(x)):
    y = predict(network, x[i])
    p = np.argmax(y)
    if p == t[i]:
        accuracy_cnt += 1

print('Accuracy: ' + str(float(accuracy_cnt) / len(x)))

批处理方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
x, t = get_data()
network = init_network()

batch_size = 100
accuracy_cnt = 0

for i in range(0, len(x), batch_size):
    x_batch = x[i:i + batch_size]
    y_batch = predict(network, x_batch)
    p = np.argmax(y_batch, axis=1)
    accuracy_cnt += np.sum(p == t[i:i+batch_size])


print('Accuracy: ' + str(float(accuracy_cnt) / len(x)))