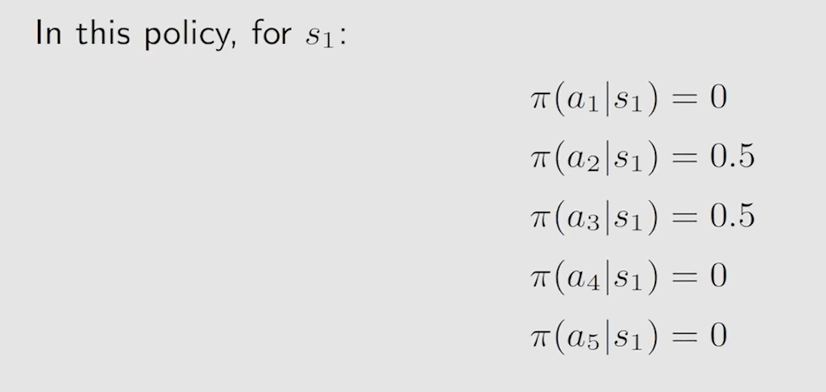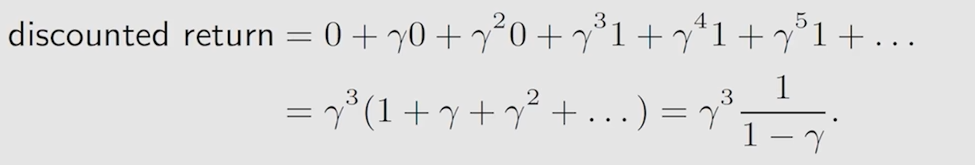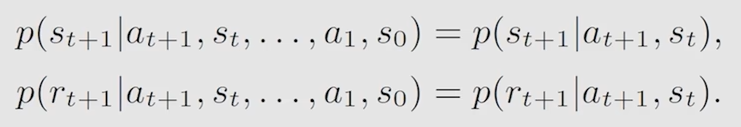RL的基本数学原理—基本概念
State
它是agent相对于当前环境的一个状态,如当前的坐标 (x,y),速度、加速度等
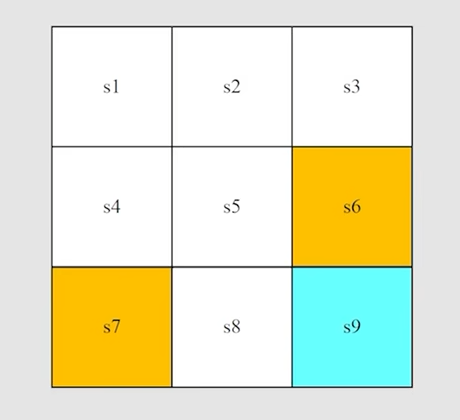
所有的状态构成的一个集合称之为状态空间,如下图,s1~s9构成了一个状态空间,这里是2D的,那么状态主要就是location (x, y)
Action
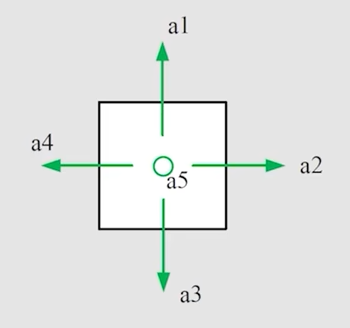
在每一个状态下,都会有对应的一系列的动作Action,如2D平面上,在一个状态下可以采取的Action有前进、后退、左右移动、原地不动
所有的Action构成的一个集合就称之为动作空间 Action space
Action 和 state 是相互依赖的,不同的状态下对应不同的动作
$$
A(s_i) = {a_i}
$$
上式意为,在状态 s_i 下,可采取的动作 a_i
State transition
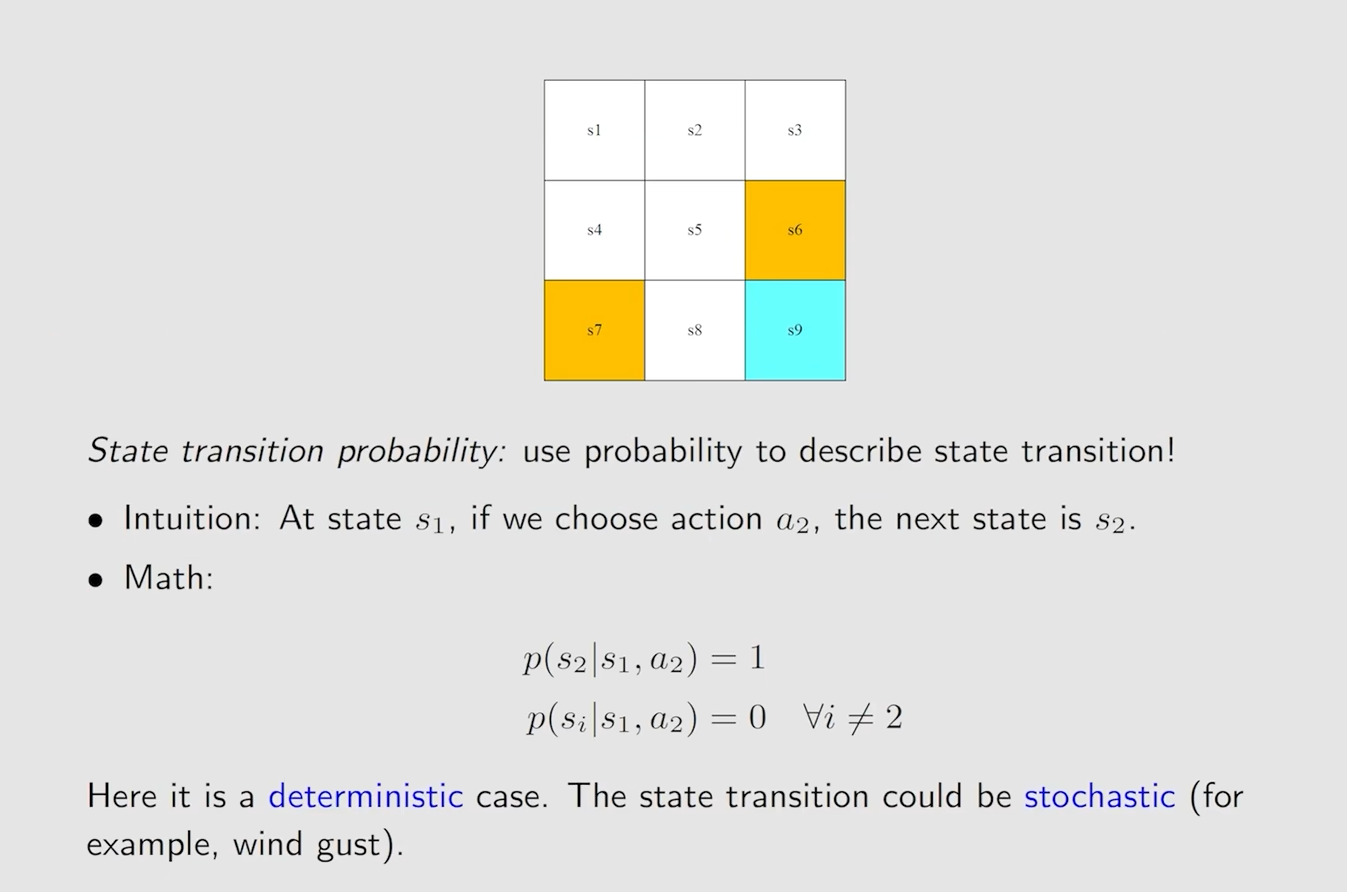
状态转换,在当前状态 s1 下,采取动作 a2(有概率采取动作 a2),会转换到下一状态 s2,而这个下一状态 s2,其实是不确定的,它根据采取的动作而定,而且只是有概率转移到某个状态 s
$$
s_1 \xrightarrow{a_2} s_2
$$
状态转换定义了 agent 与环境交互的一种行为在某个状态下,采取某个动作就直接确定的转换到某个状态,这种情况就类似于拓扑图,但实际上不是这样
实际中,在一个状态下,采取的动作都是有概率的,如在 s1 下,可以采取 a1、a2、a3 三种动作,但是这三个动作都是有概率的,p(a1)=p(a2)=0.3,p(a3)=0.4,并且每个动作对应的转换状态(下一状态)也可能是多个且一样的有概率,如采取 a1,对应的状态有s2、s3、s4,概率也是0.3、0.3、0.4,这样,事情就变得复杂多样了
State transition probability
这里采用了条件概率来描述 state transistion 的过程,这是一个随机性的例子(deterministic case)
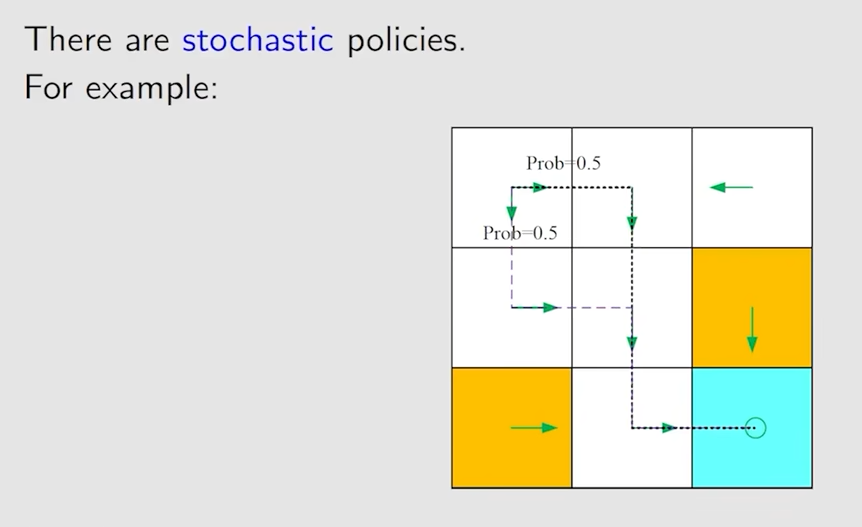
Policy
它的作用是“指示” agent 在某个状态 s 下应该采取什么 Action
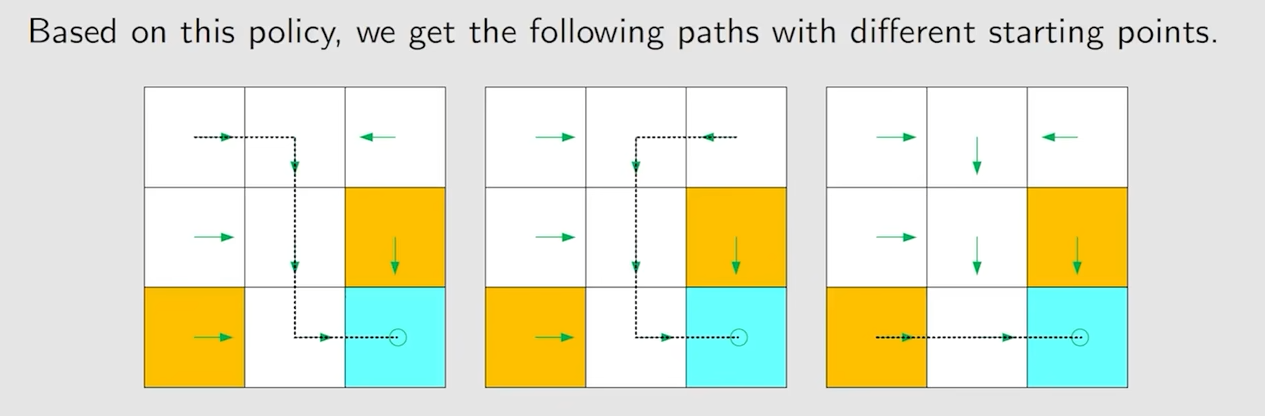
这样一条路径path或者说 trajectory 就是一种策略 policy
策略同样还是用条件概率来表示
不过上面的策略是一种确定性的策略,也就是在状态 s1 下,一定会采取动作 a2,并非随机性的,下面的就是随机性的策略了
其条件概率就是这样的了
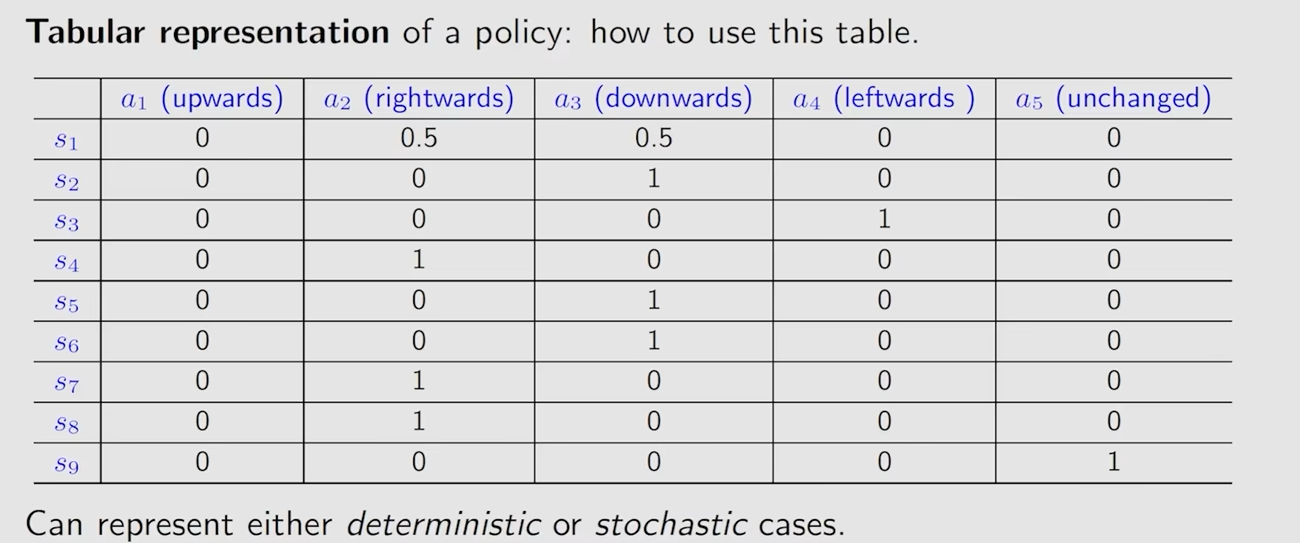
通常概率为零的就会省略掉,策略可以通过一个表格来表示,这种表格既能描述确定性的情况,也能描述随机性的情况
对应的代码实现,通常是用数组或者矩阵来存储这个表格以表示某个策略,通过对(0,1)这个区间进行随机采样,以 s1 为例,若 x 属于 (0,0.5) 就采取a2,若 x 属于 (0.5,1) 就采取 a3
Reward
首先它是一个数,一个标量,agent 在当前状态下采取了一个动作Action,会得到一个奖励 reward,如果 reward 值为正,代表鼓励该行为(Action),否则就是惩罚该行为(Action)
reward 是 agent 与人交互的一种手段,因为这个奖励机制是人为设定的,通过设定合适奖励机制引导 agent 达到预期的效果,同样的可以用条件概率来表示
$$
p(r=-1|s_1,a_1)=0.6,p(r \neq -1|s_1,a_1)=0.4
$$
获得 reward 的多少不是一层不变的,通常会有一个衰减系数来控制reward 依赖于当前状态 s 以及在当前状态下采取的动作Action
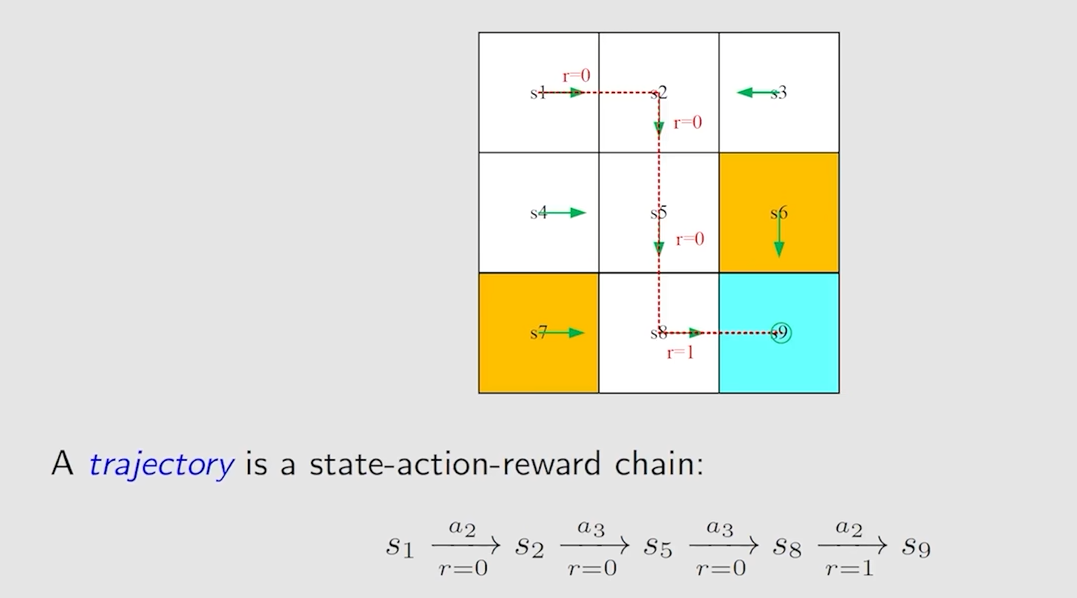
Trajectory and return
Trajectory 是一条 状态 state–>动作 Action–>奖励 reward 的链,具体例子如下图所示
return 就是一个 trajectory 上所有 reward 之和,上面的 return = 0 + 0 + 0 + 1 = 1
trajectory的优劣或者说策略policy的优劣是与其对应的return相关的
discounted return
为了获得尽可能多的奖励 reward 和总的奖励 return,一条trajectory可能会无限进行下去,return最终会发散,如下图
这就引入一个discount rate,通常用 γ 表示,γ 在[0,1)之间,discount rate 与 return 结合就得到了 discount return
当 γ < 1 时,这个无穷数列的和就等效于右边的 1/( 1 - γ)
通过引入这个衰减因子 γ,就使得 return 从一个发散状态,变成一个有限值 discount return。
另外,当 γ 趋于 0 时,那么随着 γ 的次幂越来越高,会很快的衰减至0,return 的值就主要取决于前面几项;而 γ 趋于 1 时,后面的项衰减会慢很多。换句话说,γ 越小,越注重当前或者未来临近的状态-动作-奖励,而 γ 越大,则是注重更长远的策略
episode
episode属于trajectory的一种,当 agent 采用某种策略时,它可能达到最终状态(terminal state)后就停下来了,不会一直进行下去,更不会使return发散,它是有限的,这样的任务也称之为 episodic tasks
有些任务是没有最终状态,它会无限的进行下去,称之为 continuing tasks
MDP
马尔可夫框架
三个集合:状态集合 S、动作集合A(s)、奖励集合R(s,a)
两个概率分布(条件概率?):状态转换的条件概率 p( s’ | s, a)、奖励的条件概率 p( r | s, a)
策略:Π( a | s )
马尔可夫性质:memoryless property,历史无关性
下一状态只取决于当前状态,以及当期状态下采取的动作,奖励也是如此
如果马尔可夫过程 Markov process 的策略确定下来了,那马尔可夫过程就变成了马尔可夫决策过程 Markov decision process